I’ve been working with K-5 teachers on how to use tape diagrams to solve problems. During one of these workshops, a first grader peeked in and asked, “Teachers have to go to school too?” It got quite a laugh, but it’s true. We need time to sit with our peers and try new ways to solve problems. I also think it reminds us of what it feels like to be a student and see things through a different lens.
One of the problems we worked on was:
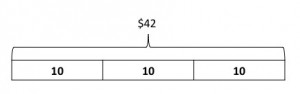
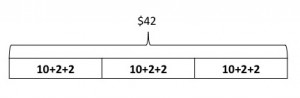
Ms. Placa spends a total of $42 for 3 sweaters. Each sweater costs the same amount. How much does each sweater cost?
Most of the groups solved this by using long division.
But let’s say you have students who don’t remember the long division algorithm (most likely because it never it held any meaning to them). If they have been working with a tape diagram or bar models, they can solve it using that.
First they can draw a bar and split it into three equal boxes to represent the 3 sweaters.
Then they can try guessing in order to determine what goes in the box. You want to work with them on using efficient strategies for guess and check. For example, 10’s are easy to count by, so they can start with 10s.
They can see that they still need 12 more. At this point, some students may know that they can divide 12 by 3 and it will give them 4. If not, they can count by 2’s and then by 2’s again.
When they add what is in each box, they get to $14 for each sweater.
The tape diagrams may seem strange to us at first if we haven’t used them before. We need to learn how to use them just like students need to learn how to use them in a meaningful way. However, once they do, the bar models begin to make sense to them. Later, the models can be used to build to the algorithm so that the algorithm will have meaning for them.
Research shows that students can do well when they use diagrams to solve problems. However, the diagram alone does not hold magical powers. While simply putting a tape diagram alongside a word problem aided higher ability middle school students, it did not seem to aid lower level students who received no instruction on how to use the diagram. As with any model or representation, students need guidance and opportunities to foster their understanding of it.
Want to know more? Check out:
Beckmann, S. (2004). Solving algebra and other story problems with simple diagrams: A method demonstrated in grade 4–6 texts used in Singapore. The Mathematics Educator, 14(1), 42-46.
Booth, J. L., & Koedinger, K. R. (2012). Are diagrams always helpful tools? Developmental and individual differences in the effect of presentation format on student problem solving. British Journal of Educational Psychology, 82(3), 492-511.
Yancey, A. V., Thompson, C. S., & Yancey, J. S. (1989). Children must learn to draw diagrams. The Arithmetic Teacher, 36(7), 15-19.
I like this. Idea is similar to what we call “partial quotients” but I think the diagram will be the perfect way to organize the thinking, especially because kids are already familiar with using it to solve the “fraction of” problems. Can’t wait to try it out with our 4th graders.
Yes! It can be a visual way to organize partial quotients. I can’t wait to hear how it goes with the 4th graders!!
Got started today and maybe you could help us out. Using your example of $42 and 3 sweaters: what if it was changed to $42 dollars, sweaters cost $3 apiece, and you need to find out how many sweaters you could buy? So equal group vs equal sharing. In my mind the diagram would need to change. I would imagine the kids making a series of 3’s, boxing them along the way, You would need 14 boxes with three in each box. Either counting by 3s till they got to 42 or repeatedly subtracting 3 from 42. Both seemed impractical, and as the dividends grow to 3 digits even more so. And this was our debate today at lunch: should the diagram reflect the context or is it just a tool for solving a division problem and we’ll worry about the context later. I’ve also been playing around with how to transform the tape diagram into the traditional long division algorithm by rotating it 90 deg clockwise. Hard to explain using words, I may blog about this at some point.
You bring up a really important point about division. It’s much harder to visualize how many 3’s fit into (or measure) 42 as opposed to how can I split 42 into 3 groups. But I think it is important for them to try and use a diagram for both types of contexts. Then later, you can have them try to develop strategies they can use to figure out larger numbers so they don’t have to do repeated subtraction or count by 3’s.
I’m intrigued about your plan for long division. Keep me posted!!
OK, the post is finally up! Take a look and let me know what you think about rotating the diagram and trying to connect it to the traditional long division algorithm.
exit10a.blogspot.com
I’m excited to take a look!!
Pingback: Gap Filling: Division | When Math Happens
As a middle school teacher, I can say how important it is that students be able to model this both ways. In 6th grade, they utilize tape diagrams/models to divide fractions. For many students, it is easier for them to think about the related multiplication fact (ie., 42 divided into 3 groups OR how many groups of 3 in 42).
That’s great to hear Sheila. Dividing fractions is so difficult for students to understand. I’m glad to know the diagrams help out.
Pingback: SCAFFOLDING DIVISION THROUGH STRIP MODEL DIAGRAMMING | Questioning My Metacognition
Awesome!! Thank you for sharing this! I can’t wait to use tape diagrams with fractions as well!