As I’ve mentioned before, proportional reasoning is complicated. Researchers refer to it as a “watershed” concept because of its role as both the capstone of K-8 mathematics and the cornerstone of high school mathematics.
How do we begin to tackle such a complex concept?
One of the most important things students need to understand in order to begin to reason proportionally is the difference between comparing two quantities in relative (or multiplicative) terms versus in absolute (or additive) terms.
For example, say there is a group of 6 boys and 3 girls. You can compare the number of boys and girls in various ways. When you say there are 3 more boys than girls, you are using absolute or additive thinking. When you say there are twice as many boys as girls, you are using relative or multiplicative thinking. Understanding the difference between these two comparisons and what each tells you is an essential building block in being able to reason proportionally.
We know from the research that students often struggle with moving from thinking additively about situations to thinking multiplicatively. In a classic study, Hart (1982) found that two-thirds of 13-15 year olds answered the following task incorrectly
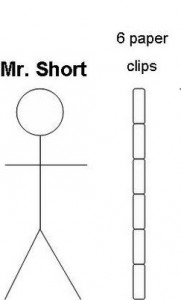
When measured with paperclips, Mr. Short is 6 paperclips tall. Mr. Short has a friend Mr. Tall. When you measure their heights with matchsticks, Mr. Short’s height is 4 matchsticks and Mr. Tall’s height is 6 matchsticks. What would be Mr. Tall’s height if you measured it in paperclips?
The majority of students who answered incorrectly said 8. They reasoned about the situation using absolute or additive thinking–adding 2 to 6. They did not see the multiplicative relationship in the situation–that Mr. Tall was one and a half times as tall as Mr. Short.
How can we begin to encourage students to think multiplicatively about situations? I’ll talk more about what the research says next time, but I’d love to hear your thoughts. If you want to know more now, check out the resources below.
Hart, K. M. (1984). Ratio: Children’s strategies and errors. A report of the strategies and errors in secondary mathematics project. London: NFER-Nelson
Karplus, R., Karplus, E., Formisano, M., & Paulson, A., (1979) Proportional Reasoning and control of variables in seven countries in J. Lochhead & J. Clements (eds), Cognitive process instruction. The Franklin Institute Press, Philadelphia.
Lamon, S. J. (2007). Rational numbers and proportional reasoning: Toward a theoretical framework for research. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning, (pp. 629-666). Reston, VA: National Council of Teachers of Mathematics.
Pingback: Proportional Reasoning: Absolute vs. Relative T...