Using Diagrams to Make Sense of Fraction Word Problems

I’ve been spending a lot of time in schools and classrooms these past two weeks using diagrams with students and teachers. As a result, I’ve been neglecting this blog but I’ve been learning so much. Hopefully, I’ll start making more time to write about what I’m doing.

Here’s the latest problem I’ve been tackling with students:

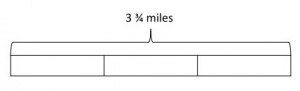
Each lap around the lake is 3 ¾ miles long. Nicora runs two-thirds of a lap and then stops.  How many miles did she run?

Some students have no idea how to get started. Others add the two fractions. Others convert the mixed number to an improper fraction and then multiply.  Of the ones who chose to multiply, many make mistakes–they convert the mixed number to an improper fraction incorrectly, they forget the rule for multiplying fractions or they forget how to convert the product to a mixed number.

Students with a strong understanding of fractions and good number sense could do the problem in their head. They thought about decomposing 3 ¾ into 3 parts and then taking two of them. The million dollar question is “why don’t the other students see the problem this way?”

In an effort to help them see the problem differently, this is how we worked on it together.

First, I asked them to tell me about the problem in their own words.  Was it about cupcakes?  Unicorns?  What is going on in the story?  I’ve found that many students need to be forced to think about what the problem is asking them to do because they are so used to circling numbers and randomly picking an operation to solve them.

I then asked them to draw a bar that shows how far a lap is.

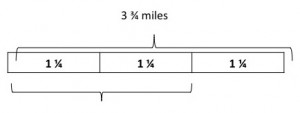
Next, I asked them to show how far two-thirds is.

Finally, I asked them to figure out how many miles two-thirds of the lap was.  Some decomposed the three and then the three-fourths.  Others used guess and check.

After we did a series of similar problems, I asked students to solve the problem without actually drawing the diagram. When they had to picture the diagram in their head, they started to develop shortcuts. One student told me that she could just divide the whole number into three and divide the fraction into three and then add them together to get the amount for one-third.  To find two-thirds, she thought about doubling the amount for one-third.

I wanted to share this example with you all because I think it shows how representations can help make explicit what may be obvious to other students. I also think it shows a nice progression of how students can use a representation to build a strategy to solve the problem.  How is this different than telling them the procedure?  Because the students build a process to solve the problem that makes sense to them.  Furthermore, they can always go back to the diagram if they forget the procedure.  So often, I find that students don’t forgot things because they are lazy, but rather because the procedure never made sense to them to begin with. My goal is to help students build on what makes sense to them, not to show them an algorithm that makes sense to me, but may not make sense to them yet.