One of the most common ways to introduce fractions to young students is to talk about ¾ as “3 out of 4.”
And it’s part of the reason why students have so much trouble with fractions later on.
Researchers Siebert and Gaskin (2006) wrote about why introducing fractions as “3 out of 4” instead of “three-fourths” creates a problematic image for students.
When the fraction three-fourths is talked about as “3 out of 4”, children picture 4 items and then taking 3 of them. The numerator and denominator are thought of as whole numbers.
The four is not a fourth. It does not refer to a certain size piece that was made by cutting up a unit into 4 equal pieces. The three does not mean 3 pieces that are one-fourth in size. The three and the four are whole numbers that happen to be written in fraction notation.
Why is thinking about the numerator and denominator as whole numbers a problem?
Here are five misconceptions that it can cause:
1. Students think the pieces can be any size. I worked with a class that had been introduced to fractions using “out of” language. When I showed them the following image, many stated that the shaded area was one-fifth because it represented “one out of five pieces” in the rectangle.
2. Improper fractions make no sense. When presented with 7/4, students are confused. How can you take 7 out of 4 items?
3. Students do not see a fraction as an amount. They have no idea where a fraction goes on a number line. For example, they might place three-fourths between 3 and 4 on the number line.
4. They apply whole number reasoning to fraction operations. Take a look at this classic mistake @mpershan posted on www.mathmistakes.org.
Students add the numerators and the denominators because they are thinking of fractions as whole numbers. It makes sense to them that having 3 out of 5 items plus 2 out of 7 items equals 5 out of 12 items.
5. They have difficulty comparing fractions. One-third is smaller than two-ninths because you only have one object instead of two objects.
It seems like a minor thing…saying “three-fourths” instead of “three out of four.” But, when combined with the models students are using to think about fractions, it can make a big difference in avoiding misconceptions later on.
I’d love to hear what you think.
Want to know more?
Siebert, D., & Gaskin, N. (2006). Creating, Naming, and Justifying Fractions. Teaching Children Mathematics, 12(8), 394-400.
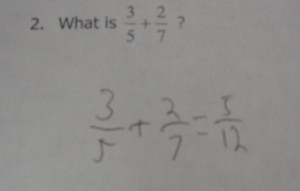
I heartily agree with you. Here in Greece, I am happy to say, this way of phrasing a fraction is not used. The only situation in which you might hear this is when you have a unit, which has been cut up into four pieces and you are asked to take 3 out of these specific 4 pieces. This is the case e.g. of a whole pie or a bar of chocolate already consisting of four bits. It wouldn’t occur if we were to consider something like 3/4 of 20 or 3/4 of 10; in that case, 3/4 would be phrased as “three fourths” (in Greek).