For those of you who think I spend the summer sipping pina coladas on the beach, you’re right—I do. Don’t be jealous. However, I also spend some of the summer going to and running professional development.
I had the chance to work with some amazing teachers this week on the fair share task I talked about last time. Here’s how it went.
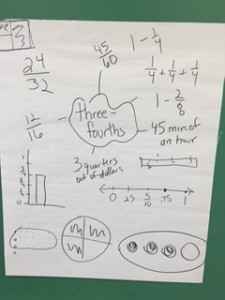
Warm Up : Today’s Number: Write or draw ¾ in as many ways as you can.
I started with this for two reasons. One was because I wanted to start a conversation about what types of tasks help engage students at the start of class. I introduced High Yield Routines as one place to get ideas from.
The other reason was that it allowed me to assess what the group’s understanding of fractions was before we went on to the fair share task. I charted out the responses the group shared out:
Pretty impressive, no? We had lots to talk about in terms of the math and in terms of using this type of activity with kids.
Fair Share Task:
After some mandatory discussions about the Danielson framework, we got to work on the task. We started with reading the problem together and making a prediction. The predictions gave me an idea of whether the group understood the task. I also was able to clarify some parts of the task, like the sandwiches being equal sizes. However, next time I think I’d change this to a notice/wonder protocol.
Teachers then worked on the task in groups of 2 or 3. Some struggled with how to start the task. I encouraged using pictures. I also had some linking cubes and paper and scissors for those who wanted to use them.
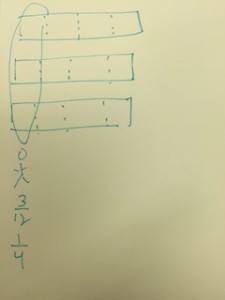
I walked around as everyone worked. An interesting misconception came up when trying to figure out how much each student ate:
One group said that when sharing 3 subs among 4 people, each person would get 3/12 of a sub. I tried to recreate the picture they drew below:
After the group explained why it was 3/12, I asked them to make a new picture that showed the reverse in order to prove their answer works. If four people each ate 3/12 of a sub, how much did they eat all together? I left them to work this out and when I came back, they changed their answer.
This misconception led to an interesting conversation about the whole. I posed the question: each student did eat three-twelfths, but 3/12 of what? A discussion about the whole had come up earlier during the warm up when someone said they we could represent three-fourths with money and use 3 quarters. Another teacher brought up the idea that when we talk about money, 3 quarters could be 3 wholes or three-fourths depending whether the whole was a quarter or a dollar. This connected nicely to our conversation here about whether one sandwich or three sandwiches were the whole.
I love the idea of using the chart as a way to prove. Here’s an example:
Gallery walk: The plan was to do a gallery walk and have everyone walk around and note whether the other groups solved the task in a similar or different way and why. Because of time and because we didn’t have a large group, we shared out the charts. An interesting conversation came up here as a group shared one of their mistakes and how they realized their strategy of how they drew the sandwiches needed to change. It was so helpful to have their thinking visible.
I shared how I often tell students they don’t have to use pencil in class. And if they do use a pencil, they should NOT use an eraser. This is always a controversial statement but the reason is that I want to see what the student is thinking at all points of the problem solving process. Plus, it encourages us to all make mistakes.
I’m still looking through the reflections that were filled out by the teachers, but I wanted to capture my reflection first. I loved the task and I think it allowed different learners to access it. Of course, I ran out of time for the rest of the activities I had planned, but I think it was worth it.
Here are some questions I’m wresting with right now:
- What’s the best way to group teachers? One participant felt uncomfortable with her math skills and being in a group of “stronger” math students didn’t help this. I had to come over several times and check in and at one point redirect the other members of the group so that her and I could chat about the math without the other group members telling her what to do. There are also teachers who do not want to work in groups and would rather work alone. I’m not sure how to address these grouping issues. Thoughts?
- How do I help teachers generalize from this task? What did we learn about engaging students in problem solving tasks? How do we transfer what we learned from this experience of doing math to teaching math?

Thanks so much for this follow up on the day! Neat to see the ‘student’ work especially.
For grouping, I’m a fan of random (both with students and teachers), though that wouldn’t necessarily solve issues like the one you described. I think group dynamics are always rough when you only have a limited time (just an hour or two). Full day PD at least allows for multiple groupings and rearrangements as activities change.
That’s a good point about the limited time. I try to mix groups up in longer PDs but even then I still struggle with when and how to rearrange.
Grouping Q: I think that we need to group teachers the same way we group students. This is important to our understanding of the grouping dynamics that are going to affect how our students work in a group. If we experience differing levels/ not wanting to work in groups/ working with different levels of interest (just like kids do!) we can look for those issues, plan for this as we group kids, develop ways to help our kids “stretch” their comfort levels in group work, and maybe even get smarter about how/why/when we group – after all, teachers are just maybe taller kids, really!
Learning from tasks Q: you commented that you will do noticing/wondering, instead of predictions. Why are you making that change? What happened in the responses to change that?
For me, delivering a lesson to teachers is about having them record their feelings/ responses to the requests. Did they feel motivated to respond? What request would have been a better motivator? Did they feel able to start the task? Why? Why not? What might they have needed first, to allow them to feel motivated/able to complete the request? All of these noticings on our part allow us to change or refine how we present a task. Those are the noticings that will allow us to motivate/ interest our students. It’s kind of like sleeping in the guest bedroom to see what our guests will experience, decide what we would need to be more comfortable, and making those changes! (Maybe that old mattress needs to go! Or add a lamp beside the chair…) Those are my thoughts – I hope this is what you were looking for!
I think the predictions turned into a notice wonder type of thing on its own and I think that part was more helpful than the predictions. So next time, I’d build that in so everyone had a chance to record what they noticed and wondered before we discussed.
I LOVE your analogy of sleeping in the guest room to have the experience so that you can plan for your guest. I try to do that with the math task because I think for many of us, this isn’t how we experienced math. Doing the activity and experiencing the math differently can help us to see things through the eyes of our students. At least that’s what I’m hoping!
I am offering to do a training for our math teachers in this type of teaching. The I,we,you is prevalent (and comfortable), but I believe we have to expand our toolbox to student centered, inquiry struggle, to really achieve the level of interest and enjoyment of learning that creates success. I would like to use some pages from your playbook, if you would allow me to.
Of course. Keep me updated on how it goes!!
I guess if they all know it’s going to be about fractions then the deep end method doesn’t work, but it would be fun to throw the main problem at them without any warm up and initially no hints or ideas. There are ways forward, one of which is quite mathematical, but looks dangerous, and that is, for a carload of 5 and only 4 subs, to imagine that there were 5 subs, so they get one each, but now they each have to cut a bit off their own whole sub to stick together and make up the extra sub and imagine handing it back. Then each cuts off a fifth, since there are 5 of them. The next group does the same, but has to cut off and return a quarter, consequently They each get less than the ones in the first group. it doesn’t need more than common sense to figure that out ! Then one can proceed to a more formal approach.
This way of looking at stuff has its parallel in geometry, where all is revealed when an extra line is introduced into the diagram(figure).
Good point about the warm up priming them that task is about fractions. There’s a tension because I wanted to get a sense of what they knew about fractions but I also didn’t want to give them any hints for the task. I probably should have done some other math work in between.
I really like the strategy you presented. I may steal it and see how a group responds to it after they’ve solved the task on their own. I love this problem because every time I discuss it someone comes up with a slightly different approach. It’s fun for a group of teachers to think about all the different informal strategies that might come up and then think about how to build on them and formalize–which for me is the basis of what I’m trying to do when I teach kids math.
ps If someone wants to work alone then I would let them do so.