Solving Multi-Step Word Problems

Recently, I was working with fourth-graders on the following word problem from the 2013 New York State test:

Ms. Turner drove 825 miles in March. She drove 3 times as many miles in March as she did in January. She drove 4 times as many miles in February as she did in January. What was the total number of miles Ms. Turner drove in February?

Let’s put aside for a minute what we think about all of this testing or the common core state standards. Let’s ignore the issue of whether or not this is a “real-world” problem or whether solving these types of problems will make students career or college ready.

Instead, let’s pretend our goal is to help students solve these types of multi-step word problems. What would you do?

When I pose that question to teachers, I often hear them tell me how they would break down the steps and explain each one to the student. That’s one strategy, but I’m going to guess that if the student sees a problem that is a little bit different, they are going to be at a loss as to what to do.

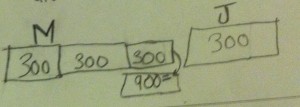
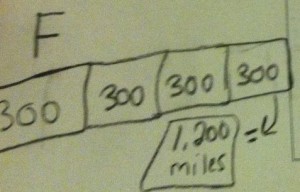
One thing I try to do when I am approaching problems like this with students is to make the numbers a little friendlier at first so I can see if the students are getting stuck because they don’t know how to think about the problem or because they are struggling with the computation. In this case, I changed 825 to 900.

Another thing I do is to encourage them to use diagrams. This problem is a great example of why I think bar models are a good tool for students.

Here’s how a student used a bar model to solve this problem.

I think that’s a pretty neat way to solve the problem. Of course, drawing and using this type of diagram is not spontaneous. Students need to have exposure to it and understand how to use it. But once they have it as a tool, they can use it to model a variety of situations.

We can talk more about how to introduce these types of models at another time and we can also talk about what the limitations are, but first I’d love to know how you would approach this problem with your students.