When I do workshops with parents, I often get complaints about why students don’t just memorize things. It’s often followed by, “I learned math that way and I’m fine!”
I then ask them to solve a multiplication of fractions problems, say 4/5 x 2/3. Inevitably, one person will tell me to draw “butterfly wings” and cross multiply. Another will tell me to find a common denominator, multiply the numerators and leave the denominators the same. Eventually, someone will say that you multiply the top and then multiply the bottom. Don’t even ask about what happens when I ask them to explain why that procedure works.
I tell this story because most of us learned multiplication of fractions without any meaning. As a result, if we forget the memorized procedure, we don’t know how to reason about it.
I’ve been using the following type of problem to help learners begin to develop meaning for what it means to multiply a fraction by a fraction.
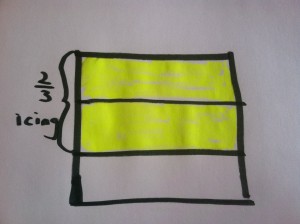
Ms. Placa made a tray of brownies. She put icing on two-thirds of the pan. She then put sprinkles on four-fifths of the brownies that had icing on them. What fraction of the pan of brownies have sprinkles and icing on them?
Before students begin, I have them estimate whether the answer is going to be bigger or smaller than two-thirds. This leads to an interesting discussion and will help addresses a major misconception later on that students have about multiplication always making things bigger.
Then students draw pictures. Here’s one possible sequence of drawings and student thinking:
1. I’ll draw a pan and shade two-thirds with icing.
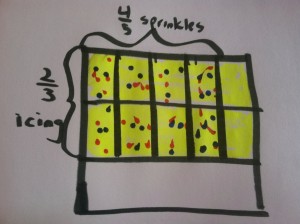
2. Now I’ll cut the iced brownies into fifths and put sprinkles on four-fifths of those.
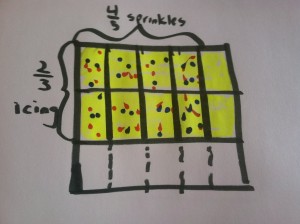
3. Hmmmm, I know I have 8 brownies with sprinkles and icing on them, but what size are they? I can’t tell because all the brownies in the pan aren’t the same size. Oh, I have to make some more cuts to have equal sized brownies.
Now I know that the brownies are fifteenths and eight of them have sprinkles and icing on them so eight-fifteenths of the pan are brownies with sprinkles and icing.
Eventually we can get to writing number sentences and to imagining what would happen with larger numbers. We can then start to generalize what rule would work for multiplying any two fractions. But I think starting with a picture and context provides a nice foundation for starting to think about multiplying fractions.
What are your thoughts? How do you usually teach students to multiply fractions?
Want to know more? The study below gives a more detailed progression of how this type of thinking was fostered and some of the background knowledge it requires.
Mack, N. K. (2001). Building on informal knowledge through instruction in a complex content domain: Partitioning, units, and understanding multiplication of fractions. Journal for Research in Mathematics Education, 32(3), 267.
It is amazing how easily students see these type of problems when you draw a picture (diagram), but there is still a disconnect with the act of taking the problem and producing a picture. I ask this each and every day, and yet yesterday I had numerous 8th graders ask, “What is a diagram?”
I love the work you have done with getting students to draw pictures about their mathematical thinking, but do you ever have them produce pictures other than circles or rectangles? I found that there is a huge stigma connected to fractions and what type of picture and thinking is associated with it.
You are so right about the difficulty students have thinking to draw the picture themselves. It takes a lot of time for them to begin to internalize the process. As for your questions about types of diagrams, I mostly use rectangles because they are easier to partition equally. Have you had success with other types of diagrams?
Rectangles are what I normally use, but I wonder if we would help student thinking if we varied that presentation. For more complex operations I could see falling back to rectangles, but I’m now curious if students would have a better background understanding of fractions if we used other types of polygons during instruction.
Earlier this year my students explored multiplying and dividing fractions using models. When I reintroduced the concept with complex fractions sadly many had forgotten the lesson.
I love visual models. My students are currently using them with ratio problems. I will love it even more when they eventually internalize it.
I’m excited to take a look at your post Mary. And I share your frustration in students not applying the models to later lessons. I think they need a lot of exposure and practice before they start to internalize it and use the visual models they have used in one situation in a new situation. I’m also interested to see what you are doing with visual models and ratio problems. Are you using bar models/tape diagrams?
Last year I spent a lot of time with my sixth graders using the bar models from the Thinking Blocks website. I moved to seventh grade this year and am reintroducing it to my students.
Another resource I use is Duane Habacker’s work with Geogebra.
What online resources do you recommend?
Thanks for sharing the resources! I must confess I don’t have any great online resources I have been using for diagrams. I have used some of the tape diagram problems from engageNY if that helps.
Love it!
Thanks Jennifer!
Pingback: Gap Filling: Fractions | When Math Happens
What you are doing here is very similar to what I do with my students and what is also modeled by our Algeblocks resource for 7th and 8th grade. Whereas they may not be creating a “real life” pictures of the brownies, they are creating a grid based on the fractions that are used in the problem.
Since you are using 2/3 X 4/5, you create a “table” 3 X 5.
You can shade 2 rows, but only covering 4 columns- thus getting 8/15.
If I could paste pictures and such I could give you a better illustration to what we do, but it is very similar, maybe I’ll post a short blog on it.
Interesting. I’d love to see the pictures. I’m also curious to hear how the kids make sense of it. Do they understand why they are making a 3 by 5 table?
OK, I wrote up a quick explanation, let me know if you have any other questions.
http://banderson02.wordpress.com/
Pingback: Multiplying Fractions via Area | MathLab
The problem is
“Ms. Placa made a tray of brownies. She put icing on two-thirds of the pan. She then put sprinkles on four-fifths of the brownies that had icing on them. What fraction of the pan of brownies have sprinkles and icing on them?”
Theory
The key word in multiplication is “of”, as in “four fifths of the brownies”.
If you go back to multiplying whole numbers, say 3 times 6, this arises from the real world situation “3 lots of 6 things in a lot”, which rapidly becomes “3 lots of 6 things”, and then “3 lots of 6”, then “3 times 6”, and finally 3×6. By now we have reached a complete abstraction of the original situation.
When we do this for fractions the real world situation (one of them) is “half of a pizza” or “half of the trayful “, and this is in effect multiplication, abstracted to “half of one”.
So the brownie problem is in reality “four fifths of two thirds of the trayful”, and there are two multiplications, with a natural order “four fifths of (two thirds of the trayful)”, or more abstractly, “4/5 of (2/3 of 1)”.
Then either by magic, or by invoking the associative rule,
we get (4/5 of 2/3) of 1, or in more symbolic form (4/5 x 2/3) of 1, which is multiplication of fractions.
What I am trying to say is that multiplication of fractions is NOT THE SAME THING as multiplication of whole numbers.
Practical
What would I do? Well, we want 2/3 of the brownies iced. The question is “How many brownies are there?”. The answer is “It doesn’t actually matter, so long as I can find 2/3 of them.”. This leads to the problem “Which numbers can you have 2/3 of?” Result, eventually: 3,6,9,12,15,18,21,….. with the 2/3’s being 2,4,6,8,10,12,14,…
Now we can address the 4/5 of the 2/3. Which if the 2/3’s can we have 4/5 of? The simplest one is 10, with 4/5 of 10 being 8.
So, finally we have 8 out of the 15 brownies with icing AND sprinkles, that is 8/15 of the brownies.
A few like this and the standard rule will make 100% sense.(which is what one is aiming for).
I love your explanation to parents who argue about why we can’t just teach the way they learned. I use 3 Act Tasks and problem solving lessons in my classroom and I completely agree, placing the skill in context and allowing students to take ownership over what they are discovering allows them to better reason their answers in more difficult problems. Thanks for sharing! This is wonderful!