Do the following tasks look familiar?
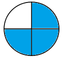
What fraction of the circle is shaded?
Shade in 2/3 of the rectangle below.
Are most of your students successful at these types of tasks? I would be willing to bet that they are after trying a couple of them.
However, I’d also guess that once you move on to more complicated concepts like comparing fractions or adding fractions, suddenly students are confused.
Why?
I think there is a misconception that if students can name a fraction in a picture and shade in a fractional amount in picture, that they understand what a fraction is. But being able to do these tasks does not necessarily mean they have a strong conceptual understanding of what a fraction is. And if they don’t have a strong foundation, topics like comparing or adding fractions is incredibly difficult.
Why can students do the tasks above yet not really understand fractions?
1. The tasks do not require students to pay attention to the equal size of the parts because they are already equally partitioned for the student. Students didn’t create the pieces themselves.
When asked to shade 2/3 of a bar that is already partitioned into 3, students can do this just by coloring in 2 boxes. They do not need to pay attention to the fact that the boxes are equal.
In fact, if given uneven size boxes, students will often shade in 2 and say that it is 2/3 because 2 are shaded and there are 3 boxes in total.
2. Young children will often focus on the shape of the pieces being the same and not on the size of the pieces being the same. Those students then have problems identifying the fraction when the pieces are equal sized but different shapes.
Van de Walle offers a great assessment problem to see what your students really understand about fractions.
Which of the shapes below are correctly partitioned into fourths? Why? Which are not correctly partitioned into fourths? Why?
Items b and c will help assess if students are focused on the number of pieces and not the size, while e and g will help assess if students are focused on the shape and not the size.
How can you avoid these misconceptions? What tasks might help develop a strong understanding of what a fraction is?
I’ll share my ideas about that in my next post, but I’d love to hear what you think.
Want to know more? Read Chapter 15 of Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2007). Elementary and middle school mathematics: Teaching developmentally.
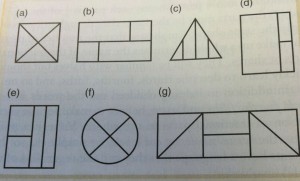
Instead of (g), or in addition to it, I might have left off its two rightmost triangles. That way there’s a rectangle cut into four equal but non-congruent parts (two rectangles and two triangles) and therefore into fourths.
Here is a task that I feel like helps students to build an understanding of fractions in a similar way. The question for each diagram is: what fraction of this shape is shaded? http://ichoosemath.files.wordpress.com/2013/08/area-sangaku-1.pdf
Thanks for the post! Looking forward to the sequel.
Hi Justin- I agree with you about the modifications to (g). I think removing the two triangles is a good idea so it’s still in four pieces. I really like the task you shared. I’d be interested to see how students approach solving them.